Nuovo saggio sulla scoperta del 4/07/2012

Pubblico qui di seguito un nuovo saggio sulla scoperta del bosone da 125 GeV compatibile con il Bosone di Higgs del Modello Standard, annunciata dagli esperimenti CMS e ATLAS dell'acceleratore LHC del CERN di Ginevra il 4 luglio scorso.

Fonte: https://docs.google.com/file/d/0B6ViMw-qiNK2YXNpcTY3aDQ2SDg/edit?pli=1

Fiocchi di neve e geometria

Dopo avervi abbondantemente deliziato con le bolle di sapone, vi voglio parlare di un'altra cosa che sicuramente vi suonerà familiare: i fiocchi di neve. Ebbene sì, anche loro nascondono i loro segreti.

Una tabella che registra alcuni dei moltissimi tipi di fiocchi di neve presenti in natura

Un cristallo di neve individuato al microscopio elettronico
a scansione all'interno di un fiocco di neve.
In secondo piano si intravedono altri cristalli
tra loro sovrapposti e orientati secondo piani differenti

I fiocchi di neve, come le impronte digitali, sono unici e diversi gli uni dagli altri.
Una domanda interessante è perché i bracci dei cristalli di neve che formano i fiocchi siano perfettamente simmetrici ed allo stesso tempo non ci siano due cristalli di neve identici. La risposta risiede nelle differenti condizioni ambientali che due cristalli diversi posti ad una certa distanza tra loro subiscono durante il processo di formazione, accrescimento e caduta ovvero nel fatto che la distanza "tra" i cristalli di neve è molto maggiore di quella "interna" al medesimo cristallo di neve.

Data la simmetria iniziale esagonale della struttura cristallina del ghiaccio comune (derivante direttamente dalla struttura molecolare dell'acqua), i bracci del cristallo di neve crescono indipendentemente in un ambiente che è ritenuto spazialmente e temporalmente molto variabile in termini di temperatura, umidità e così via. Questo ambiente è ritenuto relativamente omogeneo nello spazio di un singolo fiocco e questo porta i bracci a crescere in modo molto regolare e simmetrico, rispondendo in modo uguale a un ambiente uguale, come alberi non imparentati tra loro rispondono ai cambiamenti ambientali facendo crescere serie simili di anelli nel tronco. La differenza nell'ambiente anche minima in termini di temperatura e soprattutto umidità dell'aria su scale spaziali più grandi di quelle di un singolo cristallo di neve conduce alla mancanza di uguaglianza osservata tra le forme di due o più cristalli differenti.

Naturalmente il concetto che due cristalli di neve non possano assolutamente essere uguali è un'iperbole teorica. Infatti è perfettamente possibile, anche se improbabile, che due cristalli possano essere identici, a patto che le condizioni ambientali siano abbastanza simili: sia che i cristalli crescano abbastanza vicini l'uno all'altro sia anche per puro caso. La Società Meteorologica Americana ha riportato che due cristalli identici sono stati trovati da Nancy Knight del Centro Nazionale per la Ricerca Atmosferica il 1º novembre 1986. I cristalli non erano "fiocchi" dendritici nel senso comune del termine, ma piuttosto semplici piastre esagonali prismatiche.

In ogni caso i fiocchi di neve ci danno la possibilità di esplorare il mondo dei frattali, ovvero di enti geometrici molto particolari che ripetono la loro struttura a diversi ingrandimenti.

Il video mostra due osservazioni di cristalli di neve osservati in laboratorio per studiare le dinamiche molecolari dietro la loro formazione. Per farlo è stato usato un ago sottilissimo ad alto voltaggio che ha sostenuto poi la crescita di cristalli sulla sua punta.

Credit: Caltech/Libbrecht

  Un frattale di Mandelbrot visto a diversi ingrandimenti.

Un elegantissimo fiocco di neve: si noti le simmetrie di cui è pieno.

Per finire vi segnalo uno stupendo frattale, molto simile ad un fiocco di neve, che viene per questo chiamato Fiocco di Neve di Koch (dal nome del matematico che per primo lo descrisse nei primi del '900).
La costruzione parte da un'isola a forma di triangolo equilatero. Quindi, sul terzo centrale di ciascuno dei tre lati di lunghezza unitaria, si colloca un promontorio a forma di triangolo equilatero, dai lati uguali a 1/3. Si ottiene così un esagono regolare stellato, o stella di David, il cui perimetro ha lunghezza uguale a 4. Allo stesso modo si procede per ciascuno dei suoi dodici lati, e così di seguito, come vedete in figura.

Continuando all'infinito si otterrà la figura sottostante. Una curiosità: si potrebbe dimostrare che questa figura ha perimetro infinito, ma superficie finita.

Fonti:      

http://it.wikipedia.org/wiki/Neve

http://it.wikipedia.org/wiki/Curva_di_Koch

La matematica delle bolle di sapone

“Fate una bolla di sapone e osservatela: potreste passare tutta la vita a studiarla”

                                                                                                   (Lord Kelvin)

Una bolla di sapone, oggetto tanto semplice quanto interessante.

Chi non ha mai giocato, da piccolo, con le bolle di sapone? Di sicuro è divertente vederle scappare via e cercare di acchiapparle. Ma le bolle di sapone non sono solo un passatempo per grandi e piccini, sono anche un valido esempio di come branche astratte e affascinanti della Matematica possano essere comprese e visualizzate concretamente in fenomeni empirici.
Strettamente collegate alle bolle di sapone ci sono infatti campi della matematica come il calcolo delle variazioni (link wiki), la topologia (link wiki), le teorie dei sistemi dinamici e la teoria del caos (link wiki). Inoltre sono anche studiate dai meteorologi per le incredibili affinità tra queste e l'atmosfera terrestre.
Ma andiamo con ordine.
Prima di tutto: perché le bolle di sapone hanno proprio quella forma sferica che osserviamo?
Questo accade perché la sfera minimizza la superficie necessaria a rivestire un determinato volume, vale a dire che di tutte le superfici che delimitano solidi di volume assegnato, la sfera ha l’area minore. Curioso notare che, anche nel caso bidimensionale, la circonferenza è la curva chiusa di lunghezza minore rispetto al perimetro di qualsiasi poligono avente l'area uguale al cerchio da essa racchiuso. Questa considerazione si può inoltre estendere ad uno spazio euclideo di qualunque dimensione. Se non vi accontentate e volete una definizione rigorosa di superficie minima, eccola:

In geometria differenziale, si definisce superficie minima (o, meno usato, superficie minimale, dall'inglese minimal surface) una superficie che ha curvatura media uguale a zero in ogni punto.

Un esempio di catenoide. Anche i wormholes 
hanno una descrizione matematica simile.

Ritornando alla bolla di sapone, è importante notare come questa caratteristica geometrica della stessa sia strettamente collegata al principio fisico di minima azione o di minima energia per cui la configurazione che la bolla assume è quella che gli permette maggior stabilità con la minore energia (che, in condizioni ideali, è proporzionale all'area della sua superficie).
Se poi avete mai provato a mettere un cerchio metallico di grandi dimensioni nell'acqua saponata, vi sarete senz'altro accorti che, traslandolo in maniera ortogonale al suolo, non si forma un cilindro (come pure sembra logico che si formi) ma un altro solido, più particolare e strozzato, noto ai matematici col nome di catenoide.
Il catenoide è per l'appunto un esempio di superficie minima in quanto la sua curvatura è nulla in ogni punto.
Un altro esempio ancora è dato dall'elicoide retto, un solido molto simile ad una scala a chicciola: se prendiamo una striscia di metallo corrispondente ai bordi dell'elicoide e la immergiamo in acqua saponata, questo è il risultato che si ottiene:

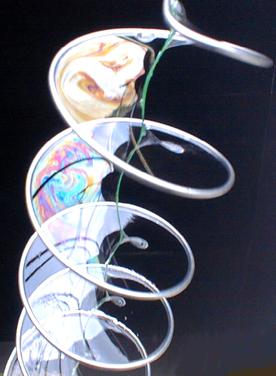Elicoide retto: l'acqua saponata si dispone in
modo da minimizzare la sua energia.

Inoltre, partendo dalla struttura del cubo ed eliminando due coppie di lati opposti delle basi, otteniamo un telaio che produce una lamina di una forma molto speciale, che ricorda proprio quella di una sella.

Una sella ottenuta con acqua saponata e una struttura opportuna.

Immergendo nell'acqua saponata un telaio a forma di cubo si ottiene la rappresentazione tridimensionale della superficie chiamata tesseratto (ovvero un ipercubo di dimensione 4), che vive nello spazio a quattro dimensioni.

Sezione tridimensionale di un ipercubo quadridimensonale, così come si
presenta nell'esperimento con l'acqua saponata.

Tutte questi modelli di superfici minime furono studiate sperimentalmente dal fisico belga Joseph Antoine Ferdinand Plateau (Bruxelles, 14 ottobre 1801 – Gand, 15 settembre 1883), che preparava lamine saponate di tutti i tipi. Durante i suoi esperimenti, Plateau riusciva sempre ad ottenere una lamina saponata, qualunque fosse la forma del telaio usato. Questi esperimenti quindi dimostravano, sperimentalmente, che le superfici minime finora conosciute non erano che una piccolissima parte delle superfici minime esistenti, delle quali bisognava però trovare le espressioni matematiche.

Visto il successo degli esperimenti di Plateau, da allora il problema di trovare la superficie di area minima avente come bordo un qualunque numero di curve chiuse nello spazio prende il nome di problema di Plateau, divenendo, di fatto, un problema di matematica pura o, al limite, di fisica matematica.

A proposito di questi temi vi segnalo questa interessante video lezione che spiega in maniera semplice tutti i concetti di base (tra l'altro evitando il formalismo matematico, per cui chiunque vi si può avvicinare):

Tutto quello che vi ho spiegato su superfici minime, calcolo delle variazioni etc.etc. lo potete guardare in questo video realizzato dal Dipartimento di Matematica dell'Università di Trento:

P.s: se non riuscite a vedere il video cliccate qui

Ma, dopo aver analizzato le bolle di sapone e le lamine saponate in scala globale, veniamo al dettaglio e occupiamoci delle chiazze di diversi colori che è possibile ammirare sulla loro superficie. I colori iridescenti della bolla di sapone sono causati dall'interazione con la luce solare dovuta in particolare alla sottigliezza del film.

Quando la luce colpisce il film, alcuni raggi sono riflessi dalla superficie esterna di questo, mentre altri penetrano all'interno e vengono riflessi solo dopo aver subito una deviazione. La riflessione che si osserva è generata dall'insieme di queste riflessioni e dalla loro interferenza. Ogni attraversamento del film da parte di un'onda di luce le fa subire uno spostamento di fase proporzionale allo spessore del film e alla frequenza del raggio di luce, e dipendente dall'angolo di osservazione. L'interferenza può essere costruttiva per alcune lunghezze d'onda e distruttiva per altre, dipendentemente dallo spessore del film. Un viraggio del colore visibile sulla superficie può essere osservato quando il film della bolla si assottiglia a causa di fenomeni locali come l'evaporazione.

Ciò significa che una bolla di sapone che flotta nell'atmosfera, poiché l'acqua presente lungo la sua superficie evapora col tempo, riflette e assorbe lunghezze d'onda diverse in diversi momenti. I film più sottili assorbono la luce rossa (maggiore lunghezza d'onda) e riflettono blu-verde (bassa lunghezza d'onda). Film ancora più piccoli assorbono il giallo e riflettono il blu e altri ancora più piccoli assorbono il verde e riflettono magenta e assorbono il blu riflettendo giallo oro. Alla fine quando il film diventa talmente sottile da essere paragonabile alla lunghezza d'onda del raggio incidente non vi è alcune riflessione sicché la bolla non presenta colorazione. A questo stadio la superficie della bolla è spessa circa 25 nm ed è sul punto di scoppiare. In realtà lo spessore del film varia continuamente perché la gravità sposta il liquido verso il basso. Ecco perché bande di colore sono spesso osservabili sulla parte bassa della bolla.

In quest'immagine è possibile notare le diverse bande di colore presenti sulla superficie di una bolla di sapone.

Siccome l'interferenza dipende dall'angolo di osservazione, anche se la superficie della bolla presenta uno spessore uniforme, si possono osservare variazioni di colore dovute al raggio di curvatura o ad eventuali movimenti.

Poiché queste bande di colore sono soggette a diversi fenomeni, il loro alternarsi e mutare forma e dimensione può essere visto come un fenomeno caotico, regolato da numerosi parametri e soggetto alle leggi stocastiche (probabilistiche) della teoria dei sistemi dinamici. Questo tipo di teorie si preoccupa, infatti, di stabilire l'evoluzione probabile di sistemi soggetti a numerosi vincoli, di vario tipo, anche chiamati perturbazioni, per cui si usa anche parlare di approcci perturbativi. Un esempio è il ''problema dei tre corpi'', in cui si vuole sapere il moto di tre corpi di massa simile e soggetti alla sola forza gravitazionale. Il problema non è mai stato risolto rigorosamente, ma ci si è sempre accontentati di soluzioni approssimate o modelli esemplificativi (ad esempio considerando due corpi con masse decisamente maggiori del terzo).

In maniera simile alle bande iridescenti di cui sopra si evolvono le correnti isobare, gli anticicloni e, più in generale, il clima terrestre. Per cui i meteorologi si servono di complessi modelli matematici molto simili a quelli usati per descrivere l'evolversi nel tempo dell chiazze colorate sulla superficie di una bolla di sapone.

Vi lascio con questo piccolo video tratto da Superquark, che introduce alcuni concetti molto noti nell'ambito della teoria del caos e con un altro video esplicativo realizzato da oilproject.com che potete guardare qui.

E per finire, alcuni link interessanti...

http://bolle.science.unitn.it/immagini.pl?0

http://bolle.science.unitn.it/   [slides]

http://en.wikipedia.org/wiki/File:Costa%27s_minimal_surface.ogv      [un tipo di superficie non ottenibile con le lamine saponate]

http://www.matematicamente.it/magazine/agosto2010/139-Dimeglio-problema-isoperimetrico.pdf  [pdf]

http://www.matematicamente.it/magazine/aprile2010/135-Zucco-isoperimetrico.pdf       [pdf]

Fonti: http://matematica.unibocconi.it/sites/default/files/Bolle%20di%20sapone.pdf

         http://it.wikipedia.org/wiki/Superficie_minima  

        http://it.wikipedia.org/wiki/Punto_di_Fermat  

       http://europa.uniroma3.it/cdlsfp_no/files/916220ff-4075-4214-ac92-0e9a5b60e29f.pdf

Sempre più pubblicazioni rafforzano la fiducia nei dati sul bosone di Higgs

I documenti rilasciati martedì dai team degli esperimenti CMS e ATLAS al Large Hadron Collider (CERN) confermano la scoperta di una particella simile al bosone di Higgs previsto dal Modello Standard.

Continua a leggere>>

La natura della nuova particella e la strana anomalia.

Di seguito riporto una lettera di R.J.Taylor del Perimeter Institute for Theoretical Physics in cui lo scienziato riflette sulla portata che potrebbe avere la recente scoperta di un bosone consistente con l'Higgs, protagonista indiscusso della conferenza tenutasi al CERN di Ginevra lo scorso 4 luglio 2012.

Nell'immagine il diagramma combinato del piccolo, appena percettibile,
 picco di frequenza di eventi correlati al canale di decadimento del candidato bosone di 
Higgs in due fotoni (canale gamma-gamma), rivelato sia dalla Collaborazione ATLAS e sia da CMS

I fisici che lavorano al CERN hanno annunciato la scoperta di una nuova particella, che è quasi certo possa essere il bosone di Higgs. Il bosone di Higgs è l'ultimo pezzo mancante del Modello Standard delle particelle e delle loro interazioni, ed è cruciale per capire perché le particelle fondamentali hanno una massa. È stato proposto per la prima volta nel 1960 ed è stato attivamente ricercato per decenni. Ora, finalmente, è stato trovato: due esperimenti sul Large Hadron Collider, denominati ATLAS e CMS, ciascuno indipendentemente, hanno annunciato che avrebbero misurato i prodotti di decadimento di una particella del peso di circa 126 GeV, ne più ne meno quanto un atomo di cesio. "Questo è un giorno sensazionale per la fisica delle particelle, il più emozionante degli ultimi decenni. L’Istituto Perimeter si congratula con il CERN e le migliaia di fisici che hanno lavorato duramente per ottenere questo risultato. Si tratta di un trionfo spettacolare e apre la porta per comprendere ciò che sta oltre il Modello Standard: dalla materia oscura ai neutrini, l'energia del vuoto, e la fisica del Big Bang. Siamo ora in grado di anticipare ulteriori scoperte", ha dichiarato il nostro Direttore, Prof. Nigel Turok. Un aggiornamento sulla strada di queste nuove scoperte arriverà nel mese di agosto, quando i fisici teorici e sperimentali della Collaborazione CMS si riuniranno all’Istituto Perimeter. La conferenza si concentrerà sui nuovi dati emersi, sulle teorie che spiegano tutti gli aspetti di questi risultati, su quali possano essere le successive misure importanti, e su ciò che è probabile si possa imparare da queste. La scoperta della nuova particella arriva attraverso l'analisi delle particelle di decadimento. Gli scienziati studiano prodotti di decadimento del bosone di Higgs, perché è molto instabile. Si è prodotto dalle collisioni ad altissima energia, come quelli del Large Hadron Collider, ma la sua vita è breve, perché dura solo una minuscola frazione di secondo – un tempo inferiore a quello che occorre ad un fascio di luce per attraversare la larghezza di un atomo - prima di decadere in una manciata di particelle secondarie. Sono queste particelle secondarie che vengono rilevate e le cui caratteristiche sono misurate dai rivelatori ATLAS e CMS. Ci sono diverse combinazioni speciali di particelle in cui il bosone di Higgs può decadere e ognuna di queste combinazioni è chiamata un "canale". Le Collaborazioni CMS e ATLAS hanno cercato la particella di Higgs in tutti i canali principali e ogni esperimento l’ha trovata nei due canali che sono stati previsti essere i più comuni. In particolare, CMS e ATLAS hanno registrato eventi in cui l'Higgs decade in due fotoni ed eventi dove l'Higgs decade in due leptoni / anti-coppie di leptoni. Essi hanno anche esaminato altri canali, ma finora non abbiamo dati sufficienti per dire qualcosa di definitivo su questi ultimi. Il prossimo passo sarà quello di misurare ogni canale con maggiore attenzione e delineare esattamente come avvengono i decadimenti della particella: in quali canali e con quali frequenze. Questo non solo per confermare che questa particella di Higgs è quella che cercavamo - come sembra quasi certo - ma anche per dirci che tipo di Higgs è. I teorici hanno un certo numero di idee in competizione sulla struttura alla base sia del Modello Standard, sia del meccanismo di Higgs. Ognuna di queste idee in competizione dà previsioni un po' diverse sulle proprietà del bosone di Higgs. Con la mappatura dei canali di decadimento – oltre ad esempio per misurarne lo spin - possiamo determinare quali sono le proprietà della particella di Higgs recentemente scoperta. L'Higgs diventa allora uno strumento per sondare la fisica oltre il Modello Standard.   È un bellissimo esempio di come l'esperimento può andare oltre la teoria. La teoria, però, può anche superare l'esperimento. Per esempio, ci sono alcuni indizi che la nuova particella appena scoperta possegga delle proprietà sorprendenti. In particolare, sembra decadere in coppie di fotoni più spesso di quanto ci si aspetterebbe. L'eccesso del canale dei fotoni (o canale gamma-gamma) è confinato entro un certo spazio molto piccolo dei diagrammi composti sul dato delle collisioni, e finora questo è solo un effetto che possiede un livello di confidenza di 1-2 sigma, nel senso che è possibile - anzi  abbastanza probabile - che si tratti di una deviazione statistica. Nel mese di aprile 2012, l’Istituto Perimeter ha ospitato una riunione di fisici provenienti da ATLAS per discutere i risultati sull’Higgs dello scorso anno e le prospettive per una maggiore precisione di misurazione dei diversi canali di decadimento. È chiaro che altri dati saranno necessari per distinguere una anomalia reale nel canale fotone dal rumore statistico. Questo richiederà del tempo. Ma non è nella natura dei fisici notare una piccola anomalia nello scoprire una nuova particella, e non prestare attenzione a tale anomalia. Ciò è particolarmente vero in questo caso, poiché l'anomalia è un eccesso in un luogo dove molte teorie prevedono un deficit. La domanda ora diventa: questo è un indizio di una nuova fisica? Se lo è, dove dovremmo cercare le prove che corroborino quest'ipotesi? I teorici avranno bisogno di costruire nuovi modelli che riproducono i risultati del CERN e cercare di vedere quali altri segnali il nuovo modello potrebbe generare. Tali segnali concordanti potrebbero quindi essere la prossima direzione di ricerca. C'è una sensazione chiara, qui all’Istituto Perimeter, ed è quella che una porta si è aperta. La particella scoperta al CERN è davvero un bosone di Higgs un po' diverso da quello che ci si sarebbe aspettato? In questo caso si potrebbe aprire una porta su una nuova Fisica. O è il bosone di Higgs del Modello Standard? Se fosse così potrebbe diventare uno strumento per sondare le teorie che stanno alla base del Modello Standard. È troppo presto per rispondere a tali domande, ma in ogni modo, l'eccitazione sta aumentando.

R.J. Taylor
Direttore delle Relazioni Esterne
Perimeter Institute for Theoretical Physics

A un passo dall'Higgs

Lo stavamo aspettando da giorni, ormai. Ed oggi, 4 luglio 2012, verso le 9 di mattina, è iniziato l'attesissimo seminario scientifico al CERN di Ginevra in cui due team separati di ricercatori hanno confrontato i dati raccolti negli ultimi mesi ai rivelatori CMS (Compact Muon Spectrometer, spettrometro compatto di muoni) e ATLAS (A Toroidal LHC ApparatuS, un apparato toroidale dell'LHC) del Large Hadron Collider, un gigantesco acceleratore di particelle circolare che si estende per 27 km sotto il territorio di Ginevra, sul confine franco-svizzero.

Continua a leggere >>

Bosone di Higgs: facciamo chiarezza.

In questi giorni i mass media non fanno altro che parlare del seminario scientifico di aggiornamento sui dati raccolti in questi ultimi mesi a LHC dagli esperimenti ATLAS e CMS che si terrà mercoledì 4 luglio alle ore 9.00 al CERN di Ginevra, proprio in concomitanza con l'ICHEP (International Conference on High Energy Physics, conferenza internazionale sulla fisica delle alte energie), la più grande conferenza di fisica delle particelle dell'anno, che si svolgerà a Melbourne dal quattro all'undici di luglio.

Continua a leggere >>

Perché il 30 giugno 2012 non è un giorno come tanti altri?

Già. Perché oggi non è un giorno come tanti? Il motivo è semplice: la giornata di oggi durerà un secondo in più delle altre. L’ultimo minuto scatterà, infatti, alle 23.59 e 60 secondi anziché alle 23.59 e 59 secondi.

IL SECONDO INTERCALARE - Questo aggiustamento temporale, puramente convenzionale, viene chiamato ''secondo intercalare'' ed è legato alla precisione degli orologi atomici che spesso non si accorda con l'irregolare rotazione terrestre. Infatti il tempo può essere misurato in diversi modi tra cui quello calcolato valutando la posizione del Sole e degli altri astri (il cosiddetto ‘tempo solare o astronomico’), più legato all'esperienza quotidiana, e quello scandito appunto dagli orologi atomici (UTC), molto più preciso e utilizzato nei centri di ricerca. Ogni tanto, però, sorge il problema di dover sincronizzare queste due misurazioni. ‘Oggigiorno – dichiara Noel Dimarcq, direttore del laboratorio Syrte, Systèmes de reference temps espace – il tempo è costruito, definito e misurato tramite gli orologi atomici che sono infinitamente stabili rispetto al tempo astronomico. Questo permette di essere sicuri che tutti attorno alla terra hanno la stessa ora’.

QUANDO LA LUNA CI METTE LO ZAMPINO - Questo ci permette di considerare un altro importante fattore che influenza il moto terrestre: la Luna. Infatti il campo gravitazionale del nostro satellite naturale è responsabile di continue (piccolissime) alterazioni dell'inclinazione dell'asse di rotazione terrestre, che causano, tra le altre cose, anche questo tipo di eventualità. Generalmente l'influenza lunare tende a far rallentare la velocità di rotazione terrestre (o comunque questo è l'effetto prevalente) per cui è più probabile avere minuti da 61 secondi piuttosto che da 59, anche se non è detto che in futuro non capiti il contrario. Inoltre, dato che il moto terrestre non è prevedibile con esattezza ma solo mediante approssimazioni - dette approssimazioni perturbative - è estremamente difficile stabilire quando ciò ricapiterà.

L’AGGIUSTATINA – A stabilire il ‘momento giusto’ è l’International Earth Rotation and Reference Systems Service (IERS) che ogni volta che lo scarto si avvicina a 0.9 secondi annuncia la necessità di ‘regolare gli orologi’. Per convenzione ‘l'aggiustatina’ avviene o all’ultimo minuto del 30 giugno o del 31 dicembre. Il primo secondo intercalare venne introdotto il 30 giugno 1972, mentre l’ultimo aggiustamento si è verificato il 31 dicembre 2008. Il periodo più lungo senza aggiustamenti è stato quello compreso fra il primo gennaio 1999 e il 31 dicembre 2005.

(ANSA)

I buchi neri vagano per l'Universo?

Anche i mostri gravitazionali possono avere il benservito. Due misteriose macchie luminose in una galassia lontana suggeriscono che gli astronomi abbiano trovato la migliore evidenza di sempre che un buco nero supermassiccio può essere spinto fuori da casa sua. Se confermata, la scoperta dovrebbe verificare la teoria della relatività generale di Einstein, in una regione di intensa gravità non precedentemente testata.
Continua a leggere >>

Gli astrofisici del Penn e la teoria della gravità ''modificata''

La maggior parte delle persone prende la forza di gravità per qualcosa di scontato. Ma per l'astrofisico Bhuvnesh Jain dell'Università di Pennsylvania, la natura della gravità è una questione vitale. Così come gli scienziati sono stati in grado di vedere più lontano e più in profondità l'universo, le leggi di gravità si sono rivelate essere sotto l'influenza di una forza inspiegabile.

Continua a leggere >>

Sono possibili interazioni tra materia oscura e corpo umano?

Per molto tempo si è creduto che l'universo fosse formato solamente dalla ''materia ordinaria''...
Continua a leggere >>

Per la prima volta alcuni fisici ricreano in laboratorio l'effetto tunnel utilizzando la luce

Gli scienziati del Cavendish Laboratory di Cambridge hanno usato la luce per aiutare gli elettroni far passare una barriera classicamente impenetrabile.
Continua a leggere >>

I coordinatori di OPERA danno le dimissioni

Un mese dopo aver rilevato errori nell'esperimento che aveva condotto alla strabiliante conclusione che i neutrini fossero più veloci della luce, i due leader della collaborazione italiana OPERA si sono dimessi.
Continua a leggere >>

Emmy Noether, questa sconosciuta...

Gli scienziati sono notoriamente molto anonimi, ma pochi possono eguagliare nelle profondità della sua oscurità perversa e immeritata il genio matematico del 20° secolo Amalie Noether.

SPL / Photo Researcher
L'innovativo teorema di Emmy Noether unisce
 due pilastri della fisica: simmetria nella natura
 e leggi universali di conservazione.

Albert Einstein la riteneva il matematico più "significativo" e "creativo" di tutti i tempi. Ha scoperto un teorema che ha unito con concisione magistrale due pilastri concettuali della fisica: simmetria nella natura e leggi universali di conservazione. Alcuni considerano il teorema di Noether, come viene ora chiamato, importante come la teoria della relatività di Einstein; esso sta alla base di gran parte della ricerca di avanguardia oggi in fisica, compresa la caccia al bosone di Higgs. Eppure Noether rimane del tutto sconosciuta, non solo per il grande pubblico, ma persino a molti membri della comunità scientifica.

Quando Dave Goldberg, un fisico della Drexel University, che si è interessato ai suoi lavori, ha recentemente fatto un sondaggio tra diverse decine di colleghi, studenti e seguaci online, è stato sorpreso dai risultati. "Sorprendentemente pochi potevano dire con esattezza chi fosse o perché fosse importante", ha detto. "Pochi altri conoscevano il suo nome ma non riuscivano a ricordare ciò che avesse fatto, e la maggior parte non aveva mai sentito parlare di lei."

Noether (pronunciato NER-ter) è nata a Erlangen, in Germania, il 23 marzo di 130 anni fa. Quindi è un bel momento per contrastare la cronica trascuratezza e celebrare la vita e il lavoro di un teorico brillante le cui passioni e il cui forte senso dell'umorismo hanno aiutato a superare gravi handicap - in primo luogo, essere donna in Germania in un'epoca in cui le università tedesche non accettavano studentesse o docenti di sesso femminile, e poi essere un pacifista ebreo nel mezzo dell'ascesa al potere dei nazisti.

Nonostante tutto questo, Noether era un matematico molto prolifico, a cui si deve la pubblicazione di papers rivoluzionarie, a volte sotto il nome di un uomo, nei campi dell'algebra astratta e della teoria degli anelli. E quando ha applicato le equazioni per l'universo intorno a lei, ha scoperto alcune delle sue regole di base, ad esempio come il tempo e l'energia sono collegati, e perché.

Ransom Stephens, un fisico e divulgatore scientifico che ha tenuto numerose conferenze sulla Noether, ebbe a dire: "Il suo teorema è la spina dorsale su cui è costruita tutta la fisica moderna".

Noether proveniva da una famiglia di matematici. Suo padre era un insigne professore di matematica presso le università di Heidelberg e di Erlangen, e suo fratello Fritz ebbe una certa fama come matematico applicato. Emmy iniziò a studiare inglese, francese e pianoforte - le materie socialmente più accettabili per una ragazza - ma il suo interesse si riversò presto sulla matematica. Esclusa formalmente dall'Università di Erlangen, Emmy frequentò ugualmente tutti i corsi, e finì per fare così bene i suoi esami finali che le fu concesso l'equivalente di un diploma di laurea.

Si specializzò all'Università di Göttingen, dove conseguì il dottorato summa cum laude e incontrò molti dei matematici più importanti dell'epoca, tra cui David Hilbert e Felix Klein, che ha fatto per la bottiglia quello che August Ferdinand Möbius aveva fatto per il nastro. La brillantezza della Noether era evidente a tutti quelli che lavorarono con lei, e i suoi mèntori maschi più volte presero la sua difesa, cercando di trovarle un posto di insegnante - meglio ancora, uno ben pagato.

"Non vedo in che modo il sesso di un candidato sia un argomento contro di esso", disse Hilbert indignato per l'amministrazione a Gottinga, dove aveva cercato di assumere Noether come l'equivalente di un professore associato. ''Dopo tutto, siamo una università, non uno stabilimento balneare". Hilbert non riuscì a risolvere il suo caso, così invece la portò sul personale come "docente ospite" più o meno permanente, e Noether,  abbastanza opportunamente, successivamente prese a nuotare in una piscina per soli uomini.

A Göttingen, ha seguito la sua passione per l'invarianza matematica, lo studio delle grandezze che possono essere manipolate in vari modi e rimanere immutate. In rapporto a una stella e al suo pianeta, per esempio, la forma e il raggio dell'orbita planetaria possono cambiare, ma l'attrazione gravitazionale lungo la congiunzione tra l'uno e l'altro rimane la stessa - e c'è l'invarianza.

http://www.nytimes.com/2012/03/27/science/emmy-noether-the-most-significant-mathematician-youve-never-heard-of.html?_r=2&pagewanted=1

Team di ricercatori vicino all'individuazione sperimentale dei fermioni di Majorana

Recentemente c'è stata una esplosione virtuale delle attività di ricerca volte ad ottenere lo sfuggente fermione di Majorana, con diversi gruppi che affermano di essere vicino alla sua scoperta.
Continua a leggere >>

I neutrini trasmettono informazioni attraverso la nuda roccia

Prima c'era il telegrafo, poi è arrivata la radio wireless, quindi la fibra ottica e ora ... i neutrini?
Continua a leggere >>

Le origini del toro nel nucleo galattico di un quasar

I quasar sono tra gli oggetti più energetici dell'universo ed alcuni di loro sono luminosi come diecimila galassie delle dimensioni della Via Lattea.
Continua a leggere >>

Il principio di Fermat

Dalla figura si evince che se un'onda colpisce la superficie di separazione di due mezzi diversi essa viene riflessa di un angolo uguale a quello d'incidenza, ma viene rifratta ( nel caso in cui  la velocità dell'onda sia maggiore nel primo rispetto al secondo mezzo) di un angolo minore.

Gli angoli sono misurati rispetto alla normale alla superficie, cioè alla retta ad essa perpendicolare.

   

Quando immergiamo un'oggetto, ad esempio una matita, nell'acqua notiamo che essa sembra ''spezzata'' in corrispondenza della superficie di separazione aria-acqua. Questo fenomeno in Fisica è conosciuto sotto il nome di rifrazione. Infatti, quando un fronte d'onda (immaginabile come l'insieme dei punti di un'onda che si trovano nella stessa fase, ovvero in configurazione di cresta, buca o una qualsiasi combinazione delle due) impatta una superficie, esso viene in parte riflesso e in parte rifratto.

Prendiamo un singolo raggio (ad es.un raggio luminoso). Come si vede dalla figura a fianco esso viene riflesso di un angolo uguale a quello d'incidenza ma viene rifratto di un angolo minore rispetto alla normale.

La matita che ''si spezza'' nell'acqua è

un esempio di rifrazione.

Il matematico francese Pierre de Fermat - molto noto per l' ''ultimo teorema'' che porta il suo nome - propose una visione alternativa di questo fenomeno. La formulazione esatta di tale principio è:

 il percorso seguito da un raggio di luce per andare da un punto ad un altro attraverso un qualsiasi insieme di mezzi è tale da rendere il suo cammino ottico uguale, in prima approssimazione, agli altri cammini immediatamente adiacenti a quello effettivo.

 Per semplificare potremmo dire (in maniera non del tutto precisa) che per andare da un punto all'altro la luce sceglie il percorso che le richiede il minor tempo possibile.

Vediamo come tramite il principio di Fermat è possibile spiegare la legge della riflessione, e per farlo consideriamo la costruzione geometrica della figura affianco.

Nella figura sono mostrati due punti A e B e uno specchio piano MM'.

Vogliamo scoprire qual è il percorso lungo il quale la luce impiega il minor tempo possibile per andare da A a B rimbalzando sullo specchio.

Illustrazione del principio di Fermat

Dal momento che tutta la traiettoria è nello stesso mezzo ottico non ci sono variazioni di indice di rifrazione: per questo motivo il tempo minore coincide anche con la strada più breve, dato che la velocità della luce rimane costante nello stesso mezzo. Si potrebbe pensare di scegliere il cammino ADB. In tal caso il segmento AD sarebbe effettivamente molto breve, ma il segmento EB risulterebbe molto lungo. Se spostiamo a destra il punto di impatto con lo specchio il secondo segmento diminuisce, mentre il primo aumenta. Per trovare il percorso più breve possiamo ricorrere a una costruzione geometrica. Costruiamo quindi dall'altra parte dello specchio un punto artificiale B' simmetrico di B rispetto allo specchio, distante quindi dallo specchio quanto B. Tracciando il segmento EB' ci si accorge che i due triangoli rettangoli EBF e EB'F sono uguali, da cui segue che EB è uguale a EB'. Il problema visto all’inizio si riduce quindi a trovare il percorso più breve per andare da A fino a B'. Ma in questo caso la risposta è ovvia, poiché il percorso più breve per unire i due punti è una linea retta. Indichiamo con C il punto in cui tale linea retta incontra lo specchio. L’eguaglianza dei triangoli ci mostra che l’angolo BCF è uguale a B'CF e quindi all’angolo ACM. Ma questo equivale proprio a dire che l’angolo di incidenza è uguale all'angolo di riflessione. La legge della riflessione è quindi una diretta conseguenza del principio del tempo minimo di Fermat.

Il Principio di Fermat e la rifrazione

Il principio di Fermat permette di avere una immediata intuizione del suo collegamento anche con la legge

della rifrazione, tenendo presente che la luce è più veloce in un mezzo di indice di rifrazione minore. Dal

punto di vista intuitivo è molto utile ricorrere all’esempio fatto da Feynman: immaginiamo che trovandoci in spiaggia nel punto A si debba salvare una persona caduta in acqua nel punto B.

Paragone intuitivo per la legge della rifrazione

Quale è il percorso più rapido per compiere tale salvataggio? 

Non la semplice linea retta da A a B, dato che siamo in grado di correre più rapidamente sulla spiaggia di quanto possiamo nuotare in acqua: dal punto di vista teorico dovremmo calcolare il percorso migliore, che comunque sarà qualcosa di simile a quello indicato in figura come ACB. Ovviamente il percorso dipende dalla nostra differenza di velocità in acqua e sulla spiaggia: allo stesso modo la luce fa un percorso che ricorda quello ACB, e a tale percorso della luce dipenderà dalla velocità della luce stessa nei vari mezzi, cioè dall'indice di rifrazione. Una  dimostrazione più rigorosa può essere effettuata utilizzando il cammino ottico.

Si noti che, osservando il percorso del raggio rifratto e tenendo presente il principio di Fermat si può prevedere, senza necessità di misure complesse, che la velocità della luce in un mezzo è minore rispetto alla velocità della luce nel vuoto.

Applicazioni del principio di Fermat

Una diretta conseguenza del principio di Fermat è il teorema di reversibilità del cammino ottico, immediatamente dimostrabile osservando che il percorso più breve all'andata lo sarà anche al ritorno.

         Foto di un miraggio

Un altro fenomeno interessante è quello del miraggio, quando nel deserto sembra di vedere una pozza d’acqua, ma anche, più semplicemente, quando si viaggia in macchina in una giornata afosa e sembra di vedere l’asfalto bagnato. Quella che in realtà vediamo è la luce del cielo riflessa sulla strada. Infatti la luce del cielo per giungere al nostro occhio può ''scegliere'' una traiettoria simile a quella illustrata in fig.1.

Questo accade poiché l’aria subito sopra la strada è molto calda, mentre in alto nell'atmosfera l’aria è più fredda e più densa, e di conseguenza riduce maggiormente la velocità della luce, che è più grande nella zona

calda. Allora la luce può ''decidere'', per arrivare al nostro occhio di non fare una linea retta, ma di percorrere più strada nella zona calda, dove va più veloce, e meno nella zona fredda in cui è più lenta, rispettando in tal modo il principio del tempo minimo. In questo modo la luce del cielo sembra provenire dalla strada, dando luogo al fenomeno del miraggio.

Fig.1: rappresentazione schematica del miraggio

Per ragioni simili quando osserviamo i corpi celesti li osserviamo generalmente leggermente più alti di quanto siano in realtà. E sempre l’effetto ”lente” dell’atmosfera fa si che il Sole sembri sorgere ad orari diversi da quelli previsti dagli almanacchi astronomici. Talvolta si può assistere al fenomeno opposto, quando l’aria al terreno è più fredda di quella negli strati superiori. È il fenomeno detto Fata Morgana, tipico ad esempio dello stretto di Messina, grazie a cui le navi sembrano sospese nel cielo . Esso prende il nome dalla leggendaria sorella di re Artù, che era in grado di costruire i suoi castelli in aria.

Forma di una lente convergente

Si pensi alla forma che assume una lente convergente: il principio di Fermat ci permette di capirne la ragione. Infatti i raggi parassiali (quelli vicini all’asse ottico) fanno un percorso maggiormente rettilineo e quindi più breve, ma percorrono un tratto più lungo nel vetro rispetto ai raggi marginali. Il tempo impiegato dai due raggi è quindi equivalente, come prevede il principio di Fermat.

Allo stesso modo la conoscenza delle proprietà di alcune curve matematiche ci permette di ricavare il comportamento di alcuni sistemi ottici. Immaginiamo ad esempio di avere una sorgente puntiforme di luce in un punto P e di voler costruire uno specchio che concentri la radiazione emessa da tale sorgente nel punto P'.

Specchio ellittico

Dato che vogliamo che tutta la radiazione si concentri in un punto e dato che i punti sono immersi nello stesso materiale (parlare di tempo e di distanza ha in questo caso lo stesso significato) si vuole trovare una superficie tale che la somma delle distanze P-superficie e superficie -P' sia una costante. Questo equivale a dire che la superficie deve essere un’ellissi di cui i due punti rappresentano i due fuochi. Proprietà simili evidenziano che uno specchio parabolico è in grado di concentrare tutta la luce che riceve da un oggetto all'infinito in un unico punto, cosa che è assai utile nei telescopi astronomici .

Qui trovate alcune applet sul principio di Fermat:

http://areeweb.polito.it/ricerca/qdbf/fil/indicegenerale/ottica/ottica_geometrica/Fermat.htm

http://www.geogebra.org/en/upload/files/italian/alessandra_tomasi/Problemi%20Ottimizzazione/Rifrazione.html

Fonti:http://www.inoa.it/home/farini/Didattica_files/fisica_lavoratori_lezione3_fermat.pdf

        http://en.wikipedia.org/wiki/Fermat%27s_principle

Alla scoperta dello stato dineutronico

Un nucleo ricco di neutroni può emetterne una coppia come singola unità come prodotto di decadimento nucleare.

Continua a leggere >>

Higgs made in USA

Dal Tevatron di Chicago arrivano novità interessanti sul famigerato bosone.
Continua a leggere >>

Alla ricerca del neutralino

Presto dal CERN potrebbero arrivare notizie di questa sfuggente particella.

Continua a leggere >>

Neutrini: tanto rumore per nulla?

Quella che sembrava una notizia sensazionale destinata a minare le fondamenta della Fisica Teorica si è rivelata un falso allarme.
Continua a leggere >>

La forma dell'Universo

''Ci sono due cose infinite: l'universo e la stupidità umana, ma riguardo l'universo ho ancora dei dubbi'' amava dire Albert Einstein. E non aveva tutti i torti. Sulla stupidità umana non mi esprimo, ma per quanto riguarda l'Universo c'è da dire che probabilmente non è infinito come si potrebbe pensare, bensì semplicemente illimitato. Anche se i due termini potrebbero sembrare equivalenti, tra di loro c'è una bella differenza.
Ma per stabilire quali sono le superfici candidate al ruolo di ''forma dell'universo'' occorrerà innanzitutto fare riferimento all'elementare quanto profondo concetto di simmetria fra tutte le dimensioni estese dell'universo: in media, infatti, tutte le direzioni dell'universo sono simmetriche.
La superficie che intuitivamente appare come la più simmetrica è senza ombra di dubbio quella di una palla, cioè la sfera bidimensionale che, in dimensione superiore, è quella che i matematici chiamano 3-sfera (superficie tridimensionale di una palla quadridimensionale). Per dirla con Brian Greene [La trama del cosmo,trad.it.,pag.286 sgg.]: ''Una caratteristica interessante della superficie sferica e di quella piatta infinita (prima ipotesi, ndr) è che ci si può camminare sopra senza mai incontrare un bordo o un confine, ma. mentre se ci s'incammina su di una palla si ritorna prima o poi al punto di partenza, su di una superficie piatta si può andare avanti all'infinito, senza trovare confini ma senza però tornare al punto di partenza. Questa sembrerebbe una differenza intrinseca fra la geometria di uno spazio curvo e quella di uno spazio piatto, ma in realtà esiste un tipo di superficie piatta che si comporta esattamente come un sfera. Per visualizzarla, pensate a un videogioco in cui lo schermo sembra essere limitato ma in realtà non lo è, perché i personaggi non possono mai uscirne o cadere giù: quando raggiungono il bordo destro riappaiono subito da quello sinistro, quando scivolano sotto il bordo inferiore riappaiono subito su quello superiore. Lo schermo sembra avvolgersi, e i bordi sinistro-destro e alto-basso vengono identificati come se fossero una cosa sola. Questa figura matematica, detta toro bidimensionale è piatta (non ha curvatura), ha dimensione finita ma non ha bordi. La versione tridimensionale di questo oggetto, cioè un toro tridimensionale, è un altro possibile candidato ad essere la forma dell'universo [...]. Questo oggetto è anch'esso piatto (nel senso che ha curvatura nulla, non nel senso che è come un foglio di carta), finito, privo di bordi e ha tre dimensioni.
C'è poi una terza possibilità per un modello che rispetti la simmetria e le osservazioni di Hubble (quelle relative all'espansione dell'universo, ndr). È difficile da spiegare in tre dimensioni, ma come nel caso della sfera ne esiste un buon esempio bidimensionale: una sella di dimensione infinita. Anche i matematici chiamano questa curva sella; è una specie di sfera al contrario, uniformemente ripiegata. Per essere precisi, la sfera ha curvatura positiva (si <<estroflette >>uniformemente verso l'esterno), la sella ha curvatura negativa (si <<introflette>> uniformemente verso l'interno) e lo spazio piano, finito o infinito, ha curvatura nulla (non si estroflette né si introflette).
I matematici hanno dimostrato che queste tre sono le uniche curvature (uniformi) possibili che rispettino i requisiti di simmetria tra tutti i punti e tutte le direzioni. Il che è davvero incredibile. Qui stiamo parlando della forma di tutto l'universo, di una cosa per cui ci immaginiamo possibilità infinite. Ma l'immenso potere della simmetria ci ha fatto restringere la ricerca a pochissime forme [...].Però non ci siamo ritrovati con una soluzione in mano, ma con tre possibilità. Visto che l'universo in cui abitiamo sembra essere uno solo, ci piacerebbe essere più specifici. Fin qui ci siamo fatti guidare dalla simmetria, e le forme che abbiamo elencato sono le uniche che rispettano il principio secondo cui ogni osservatore, qualunque sia la sua posizione nell'universo, vede a grandi scale le stesse cose. Abbiamo però visto che questo non basta per arrivare a un'unica risposta. Ora dobbiamo tirare fuori le equazioni di Einstein della relatività generale.
Le equazioni di Einstein forniscono la curvatura dello spazio a partire dalla quantità di materia ed energia dell'universo, che (le solite ragioni di simmetria) si suppongono distribuite in modo uniforme. Il problema sta nel fatto che su questo dato gli astronomi hanno discusso per decenni senza trovare un accordo. Se tutta la materia e l'energia fossero spalmati uniformemente nel cosmo e se la loro densità fosse superiore alla cosiddetta densità critica (0,00000000000000000000001 grammi per metro cubo, meglio scritti come 10^-23, cioè circa 5 atomi di idrogeno per metro cubo), allora la curvatura dell'universo sarebbe positiva; se la densità fosse minore di quella critica sarebbe negativa; e se fosse esattamente pari a quella critica sarebbe nulla. La questione deve essere ancora risolta in modo definitivo, ma gli ultimi dati più precisi sembrano far pendere la bilancia in direzione della curvatura nulla.''
L'esposizione di Greene mi sembra più che comprensibile, ma aggiungo soltanto che quando parla di curvatura si riferisce all'intero universo e non allo spaziotempo, il quale si curva localmente in presenza di materia e/o energia.


Fonti: http://it.wikipedia.org/wiki/Forma_dell'universo
         La trama del Cosmo, di Brian Greene
 

Universo o Multiverso?

Sin dalla notte dei tempi l'uomo ha sempre avuto un desiderio di conoscere lo sconosciuto e di esplorare l'inesplorato: la teoria del Multiverso rappresenta l'estrema frontiera di tale desiderio. Ma, al di là di qualunque immaginazione, l'esistenza di universi paralleli e di dimensioni extra è alla base di numerose teorie fisiche.

La stessa teoria della relatività prevede, ad esempio, una quarta dimensione (il tempo) oltre alle tre convenzionali - per cui si parla di spaziotempo quadridimensionale. Ma per avere una teoria fisica del Multiverso, cioè dell'esistenza di un insieme di universi coesistenti e alternativi, al di fuori del nostro spaziotempo, si dovrà attendere il 1957, quando il fisico Hugh Everett III pubblica uno scritto che dà il via a quella che viene chiamata interpretazione a molti mondi della meccanica quantistica.

Essa si propone di risolvere i problemi relativi al collasso della funzione d'onda e fornisce quindi una possibile risposta al paradosso del gatto di Schrödinger. Secondo l'interpretazione a molti mondi la vasta gamma di possibili posizioni di una particella si realizza in altrettanti universi e quindi in realtà esisterà un universo dove il gatto è ancora vivo e un altro dove invece è morto: il collasso della funzione d'onda non è quindi presente nè ammissibile in tale interpretazione. Cioè, quando la natura ci mette di fronte ad una serie di eventi che hanno ciascuno una determinata probabilità di accadere o meno, per questa teoria, ognuno di questi si realizza in un differente universo.

Altre teorie che avallano l'ipotesi del Multiverso sono quella delle ''bolle'', quella dell'inflazione e la già nota teoria delle stringhe.

La formazione del nostro universo da una "bolla" del multiverso venne proposta da Andrej Linde. Questa teoria è nota come teoria dell'universo a bolle. Il concetto dell'universo a bolle comporta la creazione di universi derivanti dalla schiuma quantistica di un "universo genitore". Alle scale più piccole (quantistiche), la schiuma ribolle a causa di fluttuazioni di energia. Queste fluttuazioni possono creare piccole bolle e wormhole. Se la fluttuazione di energia non è molto grande, un piccolo universo a bolla può formarsi, sperimentare una qualche espansione (come un palloncino che si gonfia), ed in seguito potrebbe contrarsi. Comunque, se la fluttuazione energetica è maggiore rispetto ad un certo valore critico, si forma un piccolo universo a bolla dall'universo parentale, va incontro ad un'espansione a lungo termine, e permette la formazione sia di materia che di strutture galattiche a grandissima scala.
 Una teoria formulata dal fisico Alexander Vilenkin afferma che il multiverso è formato da tanti universi, ognuno dei quali si trova eternamente confinato in una bolla in inflazione eterna (cioè in espansione), incluso il nostro. In alcune zone di una bolla, la deformazione dello spazio-tempo è tale da portare alla formazione di una nuova bolla, aprire un varco verso un nuovo universo; dopo un certo periodo, sempre per effetto della deformazione, la nuova bolla si stacca e si forma un universo del tutto indipendente, senza alcun punto di collegamento con quello di partenza.

Il modello inflazionario prevede che subito dopo il Big Bang ci sia stato un periodo (pochissime frazioni di secondo) in cui l'Universo si sia espanso a velocità vertiginose: questo può aver creato nuovi universi, in maniera analoga a quanto prevede la teoria delle bolle.

La teoria delle stringhe prevede una componente dello spaziotempo formata da sei dimensioni compattificate a formare una varietà di Calabi - Yau (potete vederne a lato una sezione bidimensionale che chiaramente NON è la rappresentazione di questo spazio esadimensionale): lo spaziotempo così ottenuto è nella forma M4 x V6.

Ma è con il suo sviluppo all'interno della M-teoria che si ha una vera e propria descrizione del Multiverso in quella che viene chiamata teoria del Mondo-brana.

Innanzitutto bisogna dire che la M-teoria prevede oggetti di dimensione superiore alle stringhe unidimensionali: tali oggetti vengono comunemente dette p-brane (dove brane è contrazione di membrane e p è un numero intero dallo 0 al 10). E noi vivremmo appunto in una 3-brana (una brana tridimensionale) immersa in uno spazio multidimensionale insieme ad una infinità di altre 3-brane. Occasionalmente queste brane si scontrerebbero fra loro provocando quello che localmente avrebbe gli effetti di un Big Bang (modello cosmologico ciclico). Dato che queste brane sono anche D-brane (abbreviazione di  Dirichlet-brane, dal nome dello scienziato che per primo le teorizzò) le uniche particelle che possono viaggiare da una 3-brana all'altra del multiverso sono i gravitoni (costituiti da stringhe chiuse) e non gli altri bosoni come fotoni, gluoni ecc. (costituiti da stringhe aperte) ragion per cui noi non vedremmo questi altri universi.
Ad oggi, però, l'ipotesi del Multiverso è altamente speculativa e non ci sono prove significative a suo sostegno, quindi bisognerebbe prenderla un po' ''con le pinze'': per quanto affascinante possa essere, un'ipotesi (anche se matematicamente auto-coerente) senza riscontro sperimentale non può essere ritenuta un dato di fatto.

Fonti: http://it.wikipedia.org/wiki/Multiverso
         http://it.wikipedia.org/wiki/M-teoria
         http://download.sns.it/sagnotti/Trec_fin.pdf
         http://it.wikipedia.org/wiki/Mondo-brana

Buchi neri e particelle elementari

I buchi neri sono quanto di più estremo si possa immaginare, paragonabili in questo solo al Big Bang. La loro esistenza è stata teorizzata nel 1916 dall'astronomo tedesco Karl Schwarzschild, il quale - studiando la neonata relatività generale - stabilì con esattezza la curvatura dello spaziotempo prodotta da una stella perfettamente sferica (la cosiddetta <<Soluzione di Schwarzschild>>) in un articolo che inviò allo stesso Einstein, il quale ne rimase molto colpito. Un aspetto molto interessante di questa scoperta è che, quando la massa della stella è concentrata in una regione di spazio abbastanza piccola (quando cioè il rapporto fra la massa e il raggio è superiore a un certo valore critico) il campo gravitazionale da essa generato diventa talmente grande che nulla - nemmeno la luce - può fuggire dalla sua morsa: per questo motivo fu inizialmente chiamata dark star (stella oscura), per poi essere battezzata black hole (buco nero) dal fisico John Archibald Wheeler. Vi è quindi una regione dello spazio (che nel caso più semplice coincide con la superficie di tale stella ''estrema'') andando oltre la quale non è più possibile tornare indietro e che viene perciò detto orizzonte degli eventi: qualsiasi cosa e qualsiasi informazione lo attraversi non può più uscirne e non è perciò possibile sapere cosa avvenga oltre tale orizzonte. Inoltre la regione centrale del buco nero (che dovrebbe essere adimensionale) ha curvatura infinita: non si sa precisamente che cosa accada in tale regione e quale sia il significato degli infiniti in cui ci si imbatte volendola descrivere matematicamente (curvatura infinita, dimensioni nulle ...). Questo è un caso in cui bisogna unire le equazioni della relatività generale con quelle della meccanica quantistica e pertanto il problema verrà probabilmente risolto quando si perverrà (se mai si perverrà) ad una teoria unificata di campo. A livello cosmologico, però, fioccano le ipotesi: c'è chi pensa che queste singolarità gravitazionali (così infatti viene chiamata questa regione) siano la ''porta d'accesso''ad un nuovo universo - in cui la singolarità funge da Big Bang - che ci rimarrà per sempre ignoto a causa del già citato orizzonte degli eventi.
Sembra strano ma i buchi neri - si è scoperto - non sono totalmente ''neri''. Ecco perché. Se ricordate quanto spiegato nella sezione dedicata alla termodinamica, il secondo principio della termodinamica implica che l'entropia dell'Universo è in continuo aumento. Faccio un esempio. Considerato che l'entropia è una misura del disordine di un sistema (quantitativamente sarebbe dato dal numero - precisamente dal logaritmo del numero - delle configurazioni microscopiche che lasciano invariate le proprietà macroscopiche di un sistema) immaginiamo che voi voleste riordinare la vostra camera: l'aumento di ordine della vostra stanza e quindi la sua diminuzione di entropia (motivo per il quale i cambiamenti di posizione degli oggetti sono più evidenti in una stanza ordinata piuttosto che in una disordinata) è superato dal calore che, sudando e trascinando gli oggetti, avete disperso nell'ambiente, calore che fa aumentare il moto delle molecole d'aria causando un globale aumento del disordine e quindi di entropia. Se ora ci mettessimo in prossimità dell'orizzonte degli eventi di un buco nero troveremmo che, modificando le condizioni dell'ambiente circostante, una parte considerevole di tale calore sarebbe assorbito dal buco nero, sparendo per sempre. Quindi l'entropia del sistema sarebbe diminuita. Ma ne siamo sicuri? In realtà fisici come Stephen Hawking e
Jacob Bekenstein hanno dimostrato che i buchi neri possiedono entropia e anzi sono gli oggetti più entropici dell'Universo. Questo perché tutti i buchi neri per essere individuati e classificati necessitano di soli tre parametri:

• la loro massa;
• le loro cariche di gauge (elettrica, di colore e nucleare debole o di sapore);
• il loro momento angolare.

Ma la stessa esistenza di un orizzonte degli eventi implica che qualunque cambiamento degli stati microscopici del buco nero non può essere rilevata all'esterno e quindi non provocherà cambiamenti macroscopici e - dato che maggiore è il numero di cambiamenti dei microstati che non modificano l'aspetto di un sistema cioè le sue caratteristiche macroscopiche, maggiore è la sua entropia - il buco nero ha la massima entropia possibile. Inoltre, considerata una coppia di particelle virtuali che si vengono a formare per fluttuazione quantistica nei pressi del buco nero, si potrebbe mostrare che una delle due viene inghiottita dal buco e l'altra allontanata velocissimamente dal buco. Considerando la quantità enorme di tali fenomeni si assisterà ad una vera e propria radiazione, detta radiazione di Hawking, che può anche essere vista come una radiazione di corpo nero. Il buco nero quindi irradia ed ha perciò temperatura superficiale superiore (anche se di pochissimo) allo zero assoluto.
Come abbiamo visto per identificare univocamente un buco nero abbiamo bisogno solamente di sapere massa, carica e momento angolare: le stesse caratteristiche che contraddistinguono una particella elementare (laddove il momento angolare è sostituito dallo spin) e le distinguono le une dalle altre. Questa incredibile somiglianza ha suggerito ad alcuni fisici che in realtà non ci sia alcuna differenza fra buchi neri e particelle elementari ma che siano in realtà due facce di una stessa medaglia. Ad esempio la Teoria delle Stringhe, che        
prevede particelle unidimensionali - stringhe, appunto - al posto di quelle puntiformi del Modello Standard, prevede anche che una stringa possa avere una traiettoria che spazza una superficie bidimensionale (worldsheet o foglio di universo) che si possa avvolgere attorno ad una strozzatura di una sezione della varietà di Calabi-Yau (lo spazio a sei dimensioni attorno a cui essa vibra): il foglio di universo avrebbe le caratteristiche fisiche dell'orizzonte degli eventi e la strozzatura quella della singolarità centrale di un buco nero. Ma cosa assai più particolare: diminuendo le dimensioni del foglio diminuisce la massa del buco fino ad annullarsi del tutto, diventando un fotone. Nella M-teoria, che unifica le 5 versioni della teoria delle stringhe in un quadro matematicamente coerente, ad avvolgersi attorno a questa singolarità è una membrana bidimensionale (2-brana) che funge un ruolo analogo a quello del foglio di universo e risolve anzi alcuni problemi che quest'ultimo potrebbe far insorgere: la 2-brana sarebbe quindi l'orizzonte degli eventi del buco nero che, riducendo progressivamente le sue dimensioni (e la sua massa) finirebbe per dar luogo al fotone quando la massa si annulla del tutto, analogamente al meccanismo visto prima.
Le ultime considerazioni sono teoriche, ma l'esistenza dei buchi neri e tutte le implicazioni termodinamiche (radiazione, entropia ecc.) sono ormai accettate dalla comunità scientifica: per quanto riguarda la loro esistenza, ad esempio, ci sono numerose osservazioni astronomiche indirette, che hanno dimostrato la loro esistenza esaminandone gli effetti gravitazionali, in maniera simile a quanto è accaduto in seguito con la cosiddetta materia oscura.

Fonti: http://it.wikipedia.org/wiki/Buco_nero
         http://arxiv.org/PS_cache/gr-qc/pdf/9707/9707012v1.pdf
         http://it.wikipedia.org/wiki/Orizzonte_degli_eventi
         http://it.wikipedia.org/wiki/Radiazione_di_Hawking
         http://it.wikipedia.org/wiki/Teorema_dell'essenzialit%C3%A0
         http://it.wikipedia.org/wiki/Termodinamica_dei_buchi_neri#Entropia_del_buco_nero
         L' Universo Elegante, di Brian Greene