Fisiclandia: La matematica delle bolle di sapone

“Fate una bolla di sapone e osservatela: potreste passare tutta la vita a studiarla”

(Lord Kelvin)

Una bolla di sapone, oggetto tanto semplice quanto interessante.

Chi non ha mai giocato, da piccolo, con le bolle di sapone? Di sicuro è divertente vederle scappare via e cercare di acchiapparle. Ma le bolle di sapone non sono solo un passatempo per grandi e piccini, sono anche un valido esempio di come branche astratte e affascinanti della Matematica possano essere comprese e visualizzate concretamente in fenomeni empirici.
Strettamente collegate alle bolle di sapone ci sono infatti campi della matematica come il calcolo delle variazioni (link wiki), la topologia (link wiki), le teorie dei sistemi dinamici e la teoria del caos (link wiki). Inoltre sono anche studiate dai meteorologi per le incredibili affinità tra queste e l'atmosfera terrestre.
Ma andiamo con ordine.
Prima di tutto: perché le bolle di sapone hanno proprio quella forma sferica che osserviamo?
Questo accade perché la sfera minimizza la superficie necessaria a rivestire un determinato volume, vale a dire che di tutte le superfici che delimitano solidi di volume assegnato, la sfera ha l’area minore. Curioso notare che, anche nel caso bidimensionale, la circonferenza è la curva chiusa di lunghezza minore rispetto al perimetro di qualsiasi poligono avente l'area uguale al cerchio da essa racchiuso. Questa considerazione si può inoltre estendere ad uno spazio euclideo di qualunque dimensione. Se non vi accontentate e volete una definizione rigorosa di superficie minima, eccola:

In geometria differenziale, si definisce superficie minima (o, meno usato, superficie minimale, dall'inglese minimal surface) una superficie che ha curvatura media uguale a zero in ogni punto.

Un esempio di catenoide. Anche i wormholes
hanno una descrizione matematica simile.

Ritornando alla bolla di sapone, è importante notare come questa caratteristica geometrica della stessa sia strettamente collegata al principio fisico di minima azione o di minima energia per cui la configurazione che la bolla assume è quella che gli permette maggior stabilità con la minore energia (che, in condizioni ideali, è proporzionale all'area della sua superficie).
Se poi avete mai provato a mettere un cerchio metallico di grandi dimensioni nell'acqua saponata, vi sarete senz'altro accorti che, traslandolo in maniera ortogonale al suolo, non si forma un cilindro (come pure sembra logico che si formi) ma un altro solido, più particolare e strozzato, noto ai matematici col nome di catenoide.
Il catenoide è per l'appunto un esempio di superficie minima in quanto la sua curvatura è nulla in ogni punto.
Un altro esempio ancora è dato dall'elicoide retto, un solido molto simile ad una scala a chicciola: se prendiamo una striscia di metallo corrispondente ai bordi dell'elicoide e la immergiamo in acqua saponata, questo è il risultato che si ottiene:

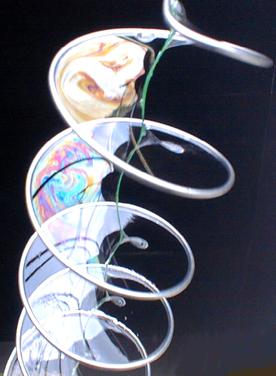Elicoide retto: l'acqua saponata si dispone in
modo da minimizzare la sua energia.

Inoltre, partendo dalla struttura del cubo ed eliminando due coppie di lati opposti delle basi, otteniamo un telaio che produce una lamina di una forma molto speciale, che ricorda proprio quella di una sella.

Una sella ottenuta con acqua saponata e una struttura opportuna.

Immergendo nell'acqua saponata un telaio a forma di cubo si ottiene la rappresentazione tridimensionale della superficie chiamata tesseratto (ovvero un ipercubo di dimensione 4), che vive nello spazio a quattro dimensioni.

Sezione tridimensionale di un ipercubo quadridimensonale, così come si
presenta nell'esperimento con l'acqua saponata.

Tutte questi modelli di superfici minime furono studiate sperimentalmente dal fisico belga Joseph Antoine Ferdinand Plateau (Bruxelles, 14 ottobre 1801 – Gand, 15 settembre 1883), che preparava lamine saponate di tutti i tipi. Durante i suoi esperimenti, Plateau riusciva sempre ad ottenere una lamina saponata, qualunque fosse la forma del telaio usato. Questi esperimenti quindi dimostravano, sperimentalmente, che le superfici minime finora conosciute non erano che una piccolissima parte delle superfici minime esistenti, delle quali bisognava però trovare le espressioni matematiche.

Visto il successo degli esperimenti di Plateau, da allora il problema di trovare la superficie di area minima avente come bordo un qualunque numero di curve chiuse nello spazio prende il nome di problema di Plateau, divenendo, di fatto, un problema di matematica pura o, al limite, di fisica matematica.

A proposito di questi temi vi segnalo questa interessante video lezione che spiega in maniera semplice tutti i concetti di base (tra l'altro evitando il formalismo matematico, per cui chiunque vi si può avvicinare):

Tutto quello che vi ho spiegato su superfici minime, calcolo delle variazioni etc.etc. lo potete guardare in questo video realizzato dal Dipartimento di Matematica dell'Università di Trento:

P.s: se non riuscite a vedere il video cliccate qui

Ma, dopo aver analizzato le bolle di sapone e le lamine saponate in scala globale, veniamo al dettaglio e occupiamoci delle chiazze di diversi colori che è possibile ammirare sulla loro superficie. I colori iridescenti della bolla di sapone sono causati dall'interazione con la luce solare dovuta in particolare alla sottigliezza del film.

Quando la luce colpisce il film, alcuni raggi sono riflessi dalla superficie esterna di questo, mentre altri penetrano all'interno e vengono riflessi solo dopo aver subito una deviazione. La riflessione che si osserva è generata dall'insieme di queste riflessioni e dalla loro interferenza. Ogni attraversamento del film da parte di un'onda di luce le fa subire uno spostamento di fase proporzionale allo spessore del film e alla frequenza del raggio di luce, e dipendente dall'angolo di osservazione. L'interferenza può essere costruttiva per alcune lunghezze d'onda e distruttiva per altre, dipendentemente dallo spessore del film. Un viraggio del colore visibile sulla superficie può essere osservato quando il film della bolla si assottiglia a causa di fenomeni locali come l'evaporazione.

Ciò significa che una bolla di sapone che flotta nell'atmosfera, poiché l'acqua presente lungo la sua superficie evapora col tempo, riflette e assorbe lunghezze d'onda diverse in diversi momenti. I film più sottili assorbono la luce rossa (maggiore lunghezza d'onda) e riflettono blu-verde (bassa lunghezza d'onda). Film ancora più piccoli assorbono il giallo e riflettono il blu e altri ancora più piccoli assorbono il verde e riflettono magenta e assorbono il blu riflettendo giallo oro. Alla fine quando il film diventa talmente sottile da essere paragonabile alla lunghezza d'onda del raggio incidente non vi è alcune riflessione sicché la bolla non presenta colorazione. A questo stadio la superficie della bolla è spessa circa 25 nm ed è sul punto di scoppiare. In realtà lo spessore del film varia continuamente perché la gravità sposta il liquido verso il basso. Ecco perché bande di colore sono spesso osservabili sulla parte bassa della bolla.

In quest'immagine è possibile notare le diverse bande di colore presenti sulla superficie di una bolla di sapone.

Siccome l'interferenza dipende dall'angolo di osservazione, anche se la superficie della bolla presenta uno spessore uniforme, si possono osservare variazioni di colore dovute al raggio di curvatura o ad eventuali movimenti.

Poiché queste bande di colore sono soggette a diversi fenomeni, il loro alternarsi e mutare forma e dimensione può essere visto come un fenomeno caotico, regolato da numerosi parametri e soggetto alle leggi stocastiche (probabilistiche) della teoria dei sistemi dinamici. Questo tipo di teorie si preoccupa, infatti, di stabilire l'evoluzione probabile di sistemi soggetti a numerosi vincoli, di vario tipo, anche chiamati perturbazioni, per cui si usa anche parlare di approcci perturbativi. Un esempio è il ''problema dei tre corpi'', in cui si vuole sapere il moto di tre corpi di massa simile e soggetti alla sola forza gravitazionale. Il problema non è mai stato risolto rigorosamente, ma ci si è sempre accontentati di soluzioni approssimate o modelli esemplificativi (ad esempio considerando due corpi con masse decisamente maggiori del terzo).

In maniera simile alle bande iridescenti di cui sopra si evolvono le correnti isobare, gli anticicloni e, più in generale, il clima terrestre. Per cui i meteorologi si servono di complessi modelli matematici molto simili a quelli usati per descrivere l'evolversi nel tempo dell chiazze colorate sulla superficie di una bolla di sapone.

Vi lascio con questo piccolo video tratto da Superquark, che introduce alcuni concetti molto noti nell'ambito della teoria del caos e con un altro video esplicativo realizzato da oilproject.com che potete guardare qui.